解説:
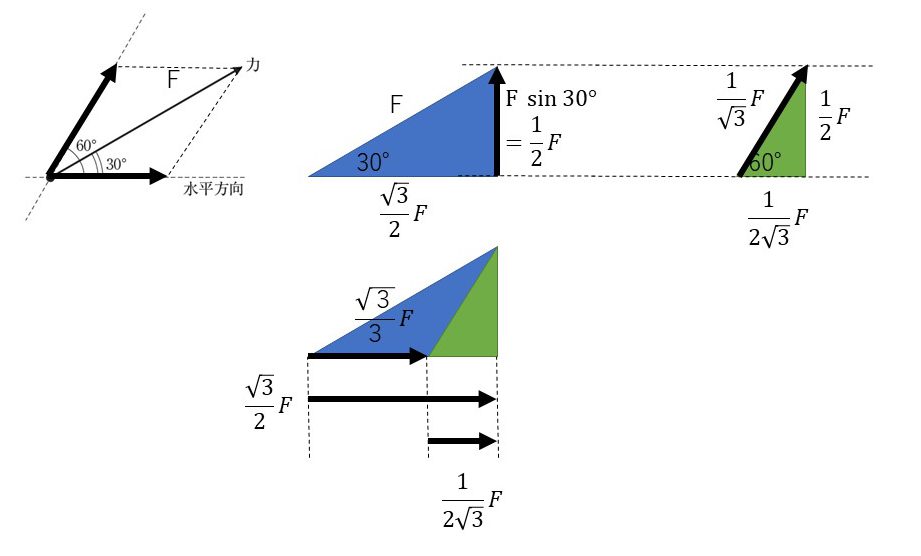
水平方向と水平より\(60^\circ\)上向きの方向に分解する場合、下図、左上のようになる。この矢印の長さを多段階に分けて求めていく。
まず、下図、中央上の青い三角形で考える。この青い三角形では、斜辺が\(F\)で、1つの角度が\(30^\circ\)の直角三角形であるので、
$$ \begin{eqnarray}
(底辺の長さ)&=&F\cos{30^\circ}\\
&=& \frac{\sqrt{3}}{2} F\\
\\
(高さ)&=& F\sin{30^\circ}\\
&=& \frac{1}{2}F\\
\end{eqnarray} $$
続いて、青の三角形の高さが\(\frac{1}{2}\)と分かったので、下図、右上の緑の三角形で、斜辺の長さと、底辺の長さを求めていく。
$$ \begin{eqnarray}
\frac{1}{2}F&=& (斜辺の長さ)\times \sin{60^\circ}\\
\frac{1}{2}F&=& (斜辺の長さ)\times \frac{\sqrt{3}}{2}\\
(斜辺の長さ) &=& \frac{1}{2}F \times \frac{2}{\sqrt{3}}\\
&=& \frac{1}{\sqrt{3}}F\\
\\
\frac{1}{2}F&=& (底辺の長さ)\times \tan{60^\circ}\\
\frac{1}{2}F&=& (底辺の長さ)\times \frac{\sqrt{3}}{1}\\
(底辺の長さ) &=& \frac{1}{2}F \times \frac{1}{\sqrt{3}}\\
&=& \frac{1}{2\sqrt{3}}F\\
\end{eqnarray}$$
ここまでで、水平より\(60^\circ\)上向きの方向の矢印の長さが
$$ \frac{1}{\sqrt{3}} $$
と分かる。
続いて、水平方向の矢印の長さを、青い三角形と緑の三角形を下図、下の中央のように重ねることで求めていく。
$$ \begin{eqnarray}
(水平方向の矢印の長さ) &=&(青の三角形の底辺の長さ) – (緑の三角形の底辺の長さ) \\
&=& \frac{\sqrt{3}}{2}F &-& \frac{1}{2\sqrt{3}}F\\
&=& \frac{\sqrt{3}}{2}F &-& \frac{1\times \sqrt{3}}{2 \sqrt{3}\times \sqrt{3}}F\\
&=& \frac{\sqrt{3}}{2}F &-& \frac{\sqrt{3}}{6}F\\
&=& \frac{3\sqrt{3}}{6}F &-& \frac{\sqrt{3}}{6}F\\
&=& \frac{2\sqrt{3}}{6}F\\
&=& \frac{\sqrt{3}}{3}\\
\end{eqnarray}$$
解説:
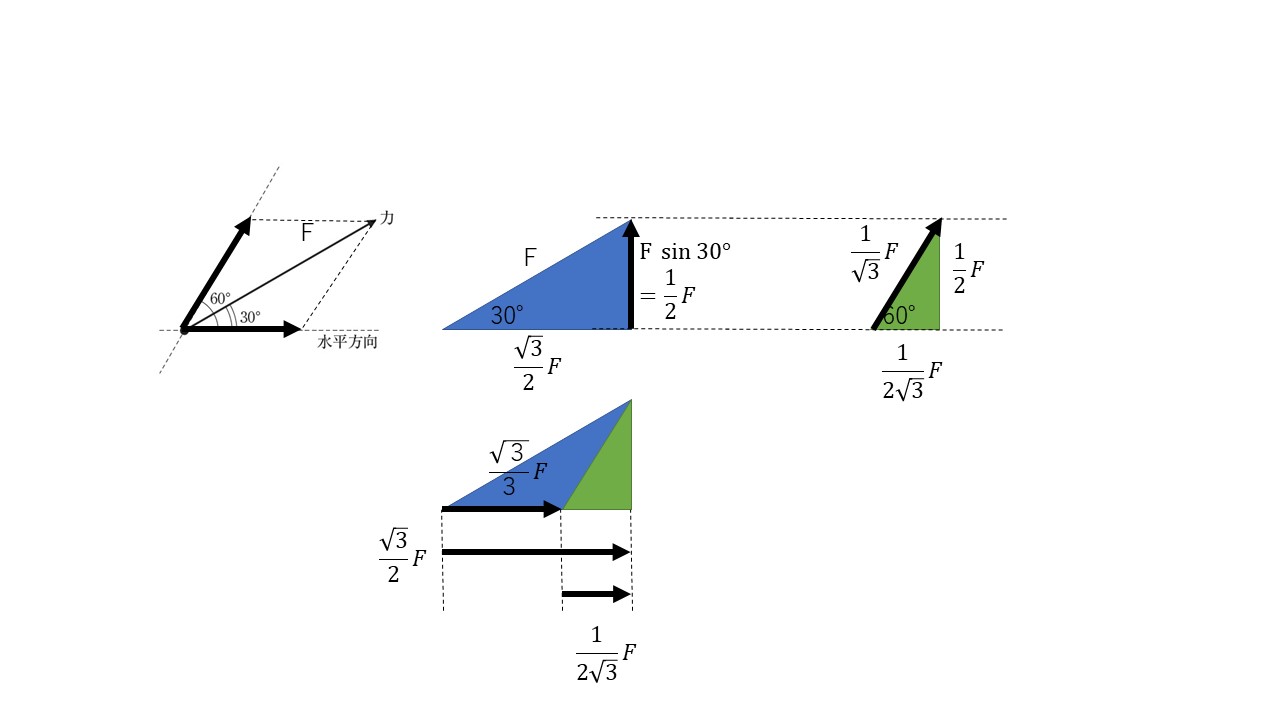
『水平方向と水平より\(60^\circ\)上向きの方向に分解する。』ということは、上図左上のような分解となる。この太矢印の長さを求めていく。
まず、青の直角三角形で、斜辺の長さが\(F\)であり、左下の角度が\(30^\circ\)であるので、
$$ \begin{eqnarray}
\cos{30^\circ} &=& \frac{底辺の長さ}{F}\\
底辺の長さ &=& F \times \cos{30^\circ}\\
&=& F \times \frac{\sqrt{3}}{2}\\
\\
\sin{30^\circ} &=& \frac{高さ}{F}\\
高さ &=& F \times \sin{30^\circ}\\
&=& F \times \frac{1}{2}\\
\end{eqnarray}$$