解説:
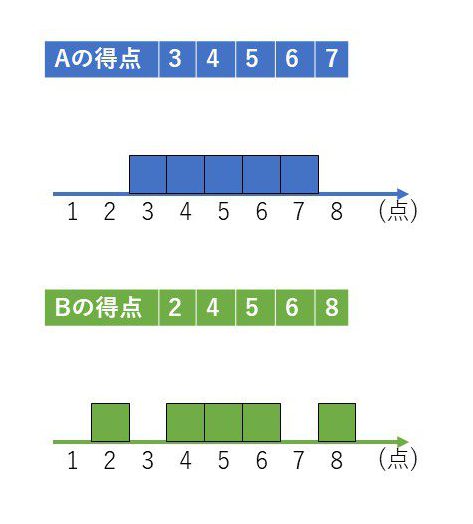
A,Bのデータを棒グラフに並べてみると分かりやすいかと思います。
平均値:
どちらも5を中心に線対称にデータが分布しているので、平均値はA, Bどちらも5点である。
分散:
Aの3点のデータがBでは2点に平均の5点から広がっている。同様にAの7点のデータがBでは、8点に広がっている。従って、AよりBの方がデータの散らばり具合が大きいので、分散はBの方が大きい。
従って、正解は④である。
念のため、計算してみる。
$$ \begin{eqnarray}
Aの平均値 &=& \frac{3+4+5+6+7}{5}\\
&=& \frac{15}{5}=5\\
\\
Aの分散 &=& \frac{(3-5)^2+(4-5)^2+(5-5)^2+(6-5)^2+(7-5)^2}{5}\\
&=& \frac{(-2)^2+(-1)^2+0^2+1^2+2^2}{5}\\
&=& \frac{4+1+0+1+4}{5}\\
&=& \frac{10}{5}=2
\end{eqnarray} $$
$$ \begin{eqnarray}
Bの平均値 &=& \frac{2+4+5+6+8}{5}\\
&=& \frac{15}{5}=5\\
\\
Bの分散 &=& \frac{(2-5)^2+(4-5)^2+(5-5)^2+(6-5)^2+(8-5)^2}{5}\\
&=& \frac{(-3)^2+(-1)^2+0^2+1^2+3^2}{5}\\
&=& \frac{9+1+0+1+9}{5}\\
&=& \frac{20}{5}=4
\end{eqnarray} $$
以上。