解説:
文章題と同じく、問題文を読んで図形がイメージできることがまず大事ですね。図は問題文についてますが、きちんと直角三角形が見えると良いです。
次に、現れた直角三角形に、[math]\sin, \cos, \tan[/math]のどれを当てはめるか考えましょう。
三角比:
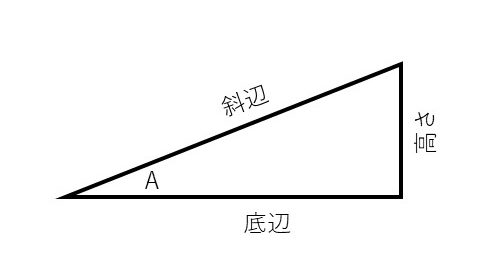
$$\sin{\angle{A}} = \frac{高さ}{斜辺}, \cos{\angle{A}} = \frac{底辺}{斜辺}, \tan{\angle{A}} = \frac{高さ}{底辺} $$
今回は、[math]\sin[/math]を当てはめると良い。
[math] \sin{\angle {B}} = \frac{AC}{AB} [/math]
[math]\angle A= 46^\circ, AB=1[/math]なので、
[math] \sin{46^\circ}= \frac{AC}{1} [/math]
[math] AC =0.7193[/math]
以上。