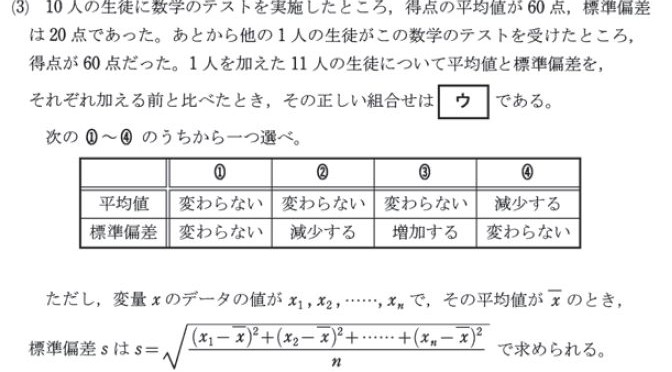
解説:
標準偏差の問題です。
標準偏差は、データの散らばり具合を表す値です。値が大きいほどデータが散らばっていることを表します。
まず、平均値がどうなるかを見てみましょう。
今回の問題では、平均値が60点のところに、60点のデータが一つ加わったので、平均値は「変わらない」ということになります。極端な例で考えてみましょう。10人の平均が60点ですので10人全員60点としてみましょう。(標準偏差の違いは無視してます)。11人目も60点であるので、11人の平均も60点ですよね。
次に、標準偏差(データの散らばり具合)がどうなるか見てみましょう。
データの散らばり具合は、平均値からどれだけ離れているかで表します。追加された11人目のデータは平均値とぴったり同じ、60点です。ということは、このデータは散らばっていません。散らばっていないデータが加わると、11個のデータ全体で見ると、散らばり具合は「減少する」ことになります。
したがって、正解は、②です。